Work done by Miro Kramar†, Arnaud Goullet†, Lou Kondic‡, Konstantin Mischaikow†
† : Rutgers University, NJ ‡ : New Jersey Institute of Technology, NJ
With the goal of extending our ability to systematically explore
network properties in greater detail, we developed rigorous
mathematical models capable of capturing geometric features
of particle interactions. The approach is based
on algebraic topology and in particular persistent homology.
This is a relatively new mathematical technique that
provides a computationally efficient rigorous framework for
multi scale analysis. The computational efficiency is
essential since the goal is to apply these techniques to
large data sets. Persistent homology reduces a scalar function
to a persistence diagram, which is a collection of points in the
plane where each point encodes well defined geometric
information about the function, but does not rely on a
particular choice of threshold to do this. In the context of
particulate systems, this means that a specific definition
of `force-chains' or similar objects is not required. Furthermore,
there are a variety of metrics that can be imposed on the space of
persistence diagrams such that in the context of particulate
systems the application of persistent homology can be interpreted
as a continuous non linear projection of the force networks to the
space of persistence diagrams. These properties of persistent
homology suggest that it is a good tool to study both the static
and the dynamical aspects of experimental and computational
realizations of particulate systems.
As indicated above, persistent homology is based on algebraic
topology and thus its computation is based on the construction of
a finite complex. The construction of appropriate complex
depends upon the type of data that is provided, which in turn is
dependent upon the method by which the data is obtained. We
propose three different complexes: digital, position,
and interaction. The information that
can be extracted via the use an interaction network is
significantly more reliable than that of a digital or position
network. The interaction network can be used in the setting
of numerical simulations or particular types of experiments where
complete information about the forces between adjacent
particles may be known. However, for many experiments only the
total force experienced by a particle may be available. This
necessitates the use of a digital or position network, depending
upon how the data is collected and physical properties of the
individual particles.
|
|
|
|---|---|---|
| Interaction network | Position network | Digital network |
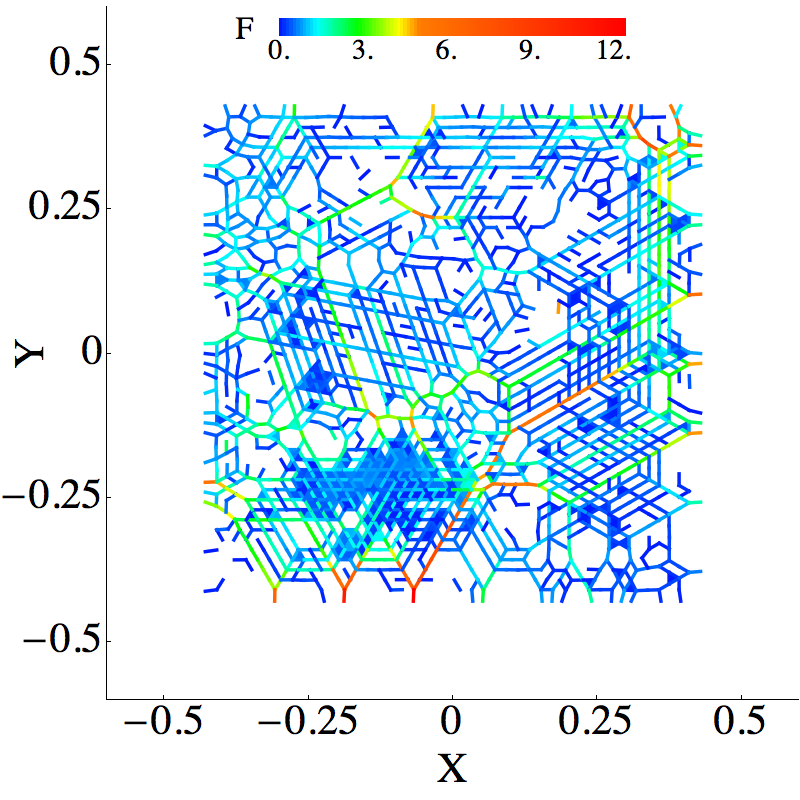
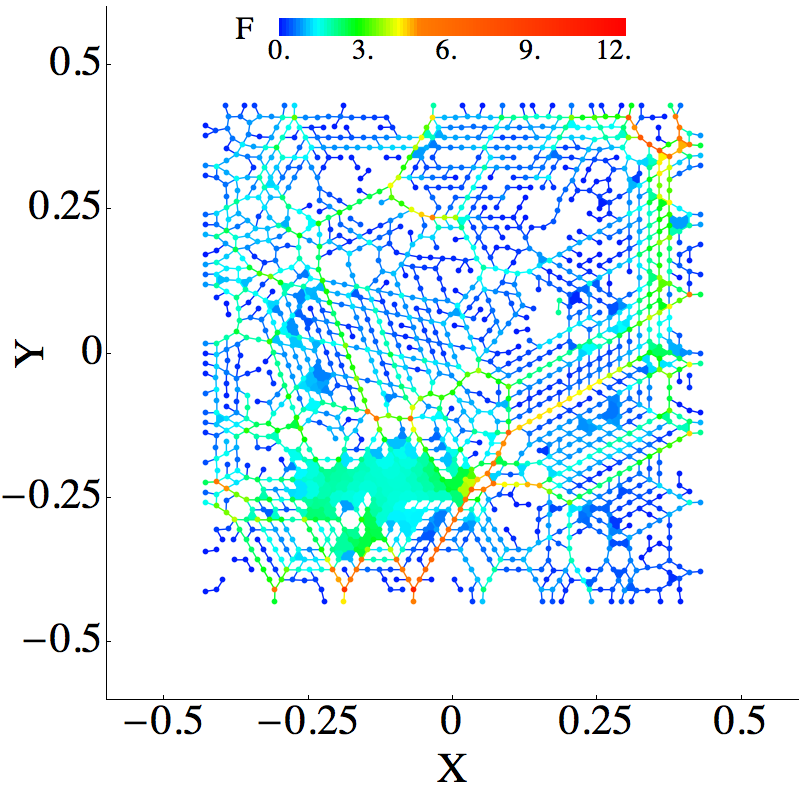
The interaction and position network can be interpreted as a real valued function on a simplicial complex. In case of the digital network the function is defined on a cubical complex which corresponds to pixels or voxels.
Interaction network
The underlying simplicial complex for the interaction network is a full 2 dimensional or 3 dimensional complex with vertices corresponding to the particles. It is every edge between any two vertices, every triangle and possibly tetrahedrons are present. The definition of the function is derived from the inter particle interactions. In our case the value of the function on the edge between two particles is a magnitude of the normal force acting between these particles. In order to extend this function to all simplecies we use the following procedure. The value at a vertex is a maximum over the edges that contain the given vertex. The value on two and tree dimensional simplecies is a minimum of the edges contained in the closure of the simplex.
Position network
The underlying simplicial complex for the position network is a 2 dimensional or 3 dimensional complex with vertices corresponding to the particles. The edge between two vertices is present if the particles are in contact. The higher dimensional simplex is present if all its edges are present. The definition of the function derived from the knowledge of some quantity assigned to the particles. In our case this quantity is the magnitude of total normal force experienced by the particles. Again the function is extended to higher dimensional simplecies by taking a minimum over the edges that are contained in their closure.
Digital network
The digital network can be constructed from a digital image by assigning the values of the pixels to the 2D dimensional cubes. Tho extend the function to the edges and vertices a minimum over the cubes containing the particular edge or vertex is taken.
Code for constructing the networks and computing their homology.
Persistent homology of the interaction network
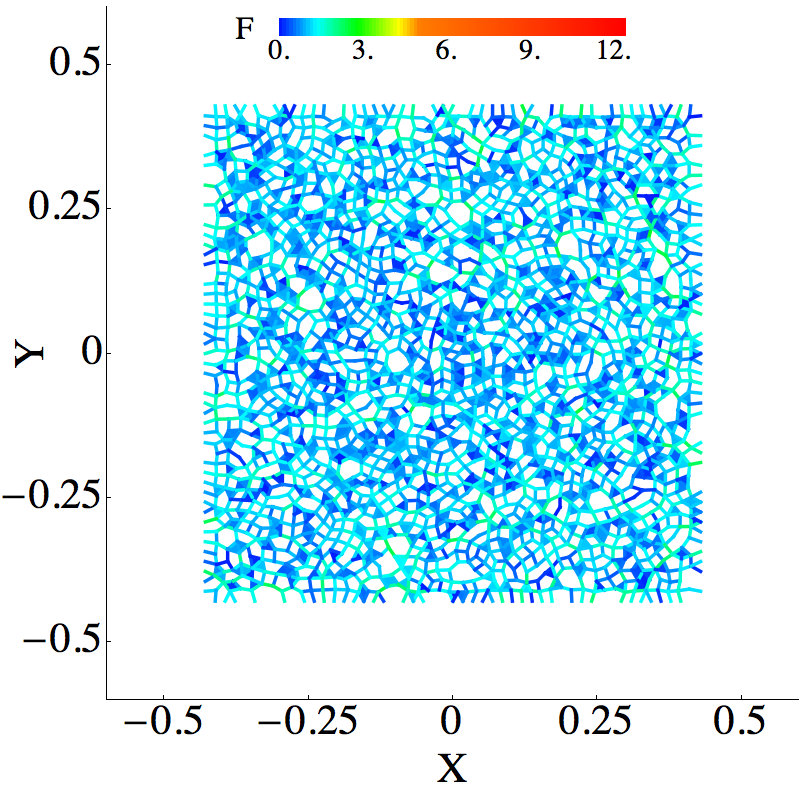
To demonstrate the power of persistence diagrams we use them to compare mono disperse frictionless system with poly disperse system with friction. Both systems are at the onset of jamming.

|
|
|
|
|---|---|---|---|
| Mono disperse system without friction | |||
|
|
|
|
| Poly disperse system with friction | |||
 We begin by assigning
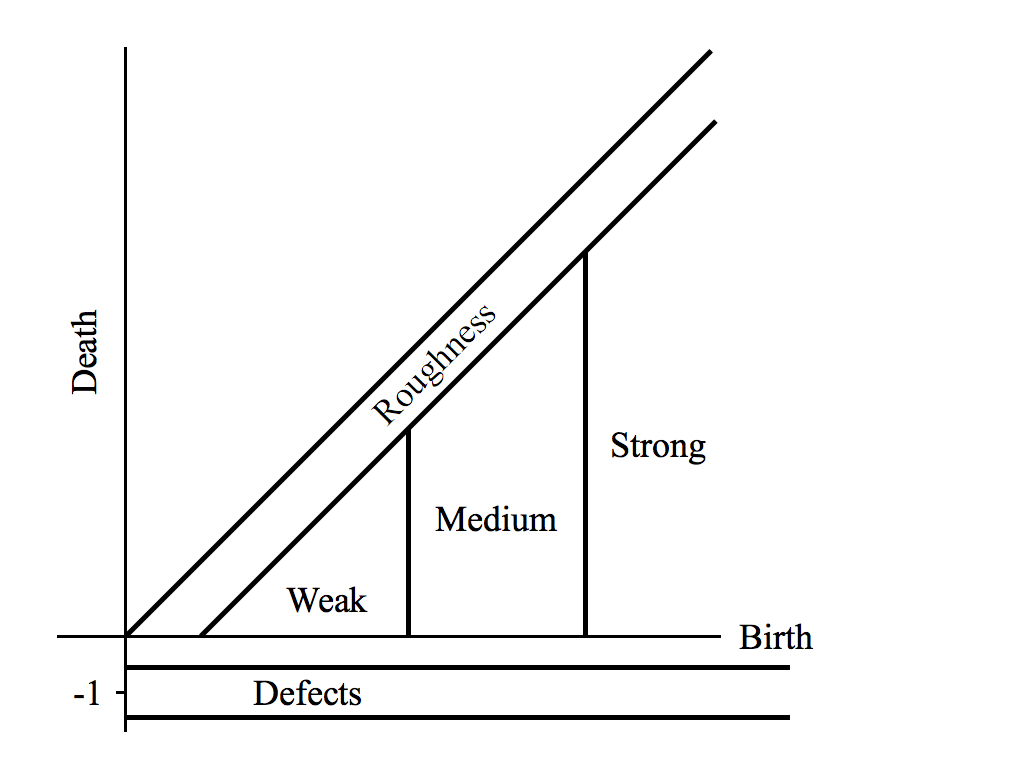
physical meaning to the location of persistence points in the
persistence diagrams. Figure on the laft shows a persistence
diagram divided into five regions. With the exception of the
region labelled defects, the location of the division lines is
intended to be either system specific or
conceptual. We explain these divisions in the context of the
interaction force networks and persistence diagrams of the shown
above. A more complete analysis of DGM using these ideas is
presented in our paper.
We begin by assigning
physical meaning to the location of persistence points in the
persistence diagrams. Figure on the laft shows a persistence
diagram divided into five regions. With the exception of the
region labelled defects, the location of the division lines is
intended to be either system specific or
conceptual. We explain these divisions in the context of the
interaction force networks and persistence diagrams of the shown
above. A more complete analysis of DGM using these ideas is
presented in our paper.
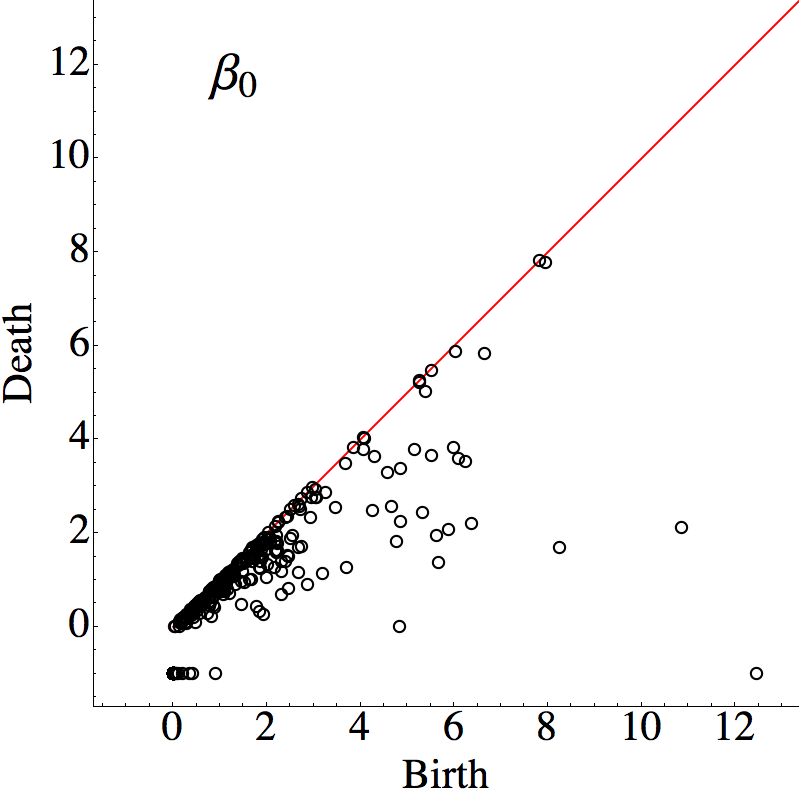
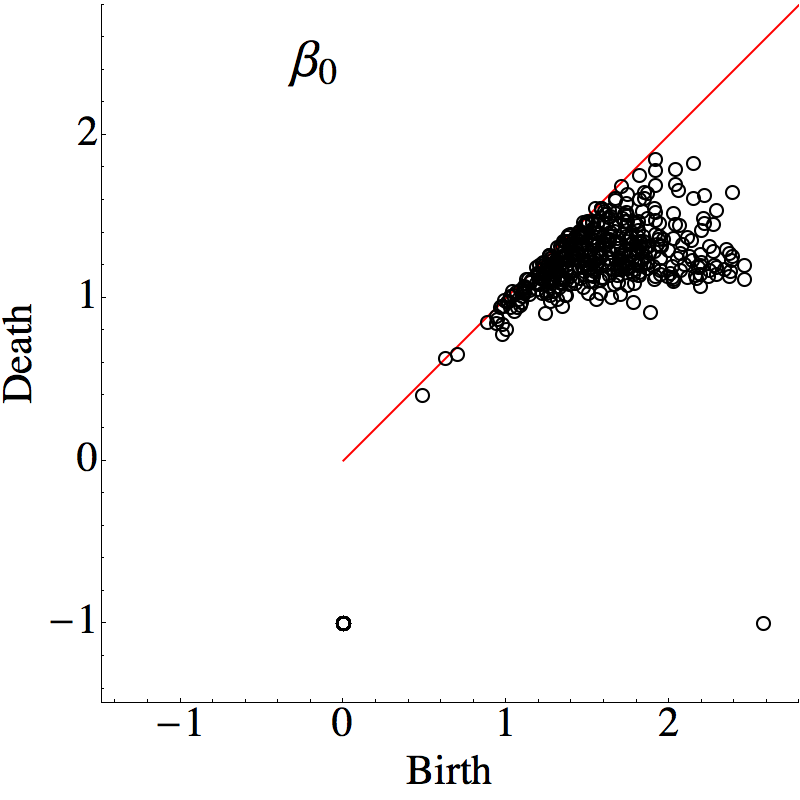
There are at least two different interpretations of the points in
the 0-dimension persistence diagram that lie close to the
diagonal; the region we have labelled as roughness. The first is
to treat this as noise, i.e. a byproduct of the imperfect
measurements of the normal forces between particles. While this
may be appropriate for many experimental settings, the data
represented here comes from numerical simulations. Thus, the
errors are extremely small compared to the size of the normal
forces. This leads to the second interpretation, which we
adopt, that this region of the persistence diagram provides a
measurement of how rough or bumpy the normal force landscape is,
e.g. should we view the surface of the landscape as being made of
glass or sandpaper? Alternatively, the points in the 0-dimension
persistence diagram that lie outside the roughness region provide
a means of measuring how non-uniform the normal force
landscape is. Therefore by comparing the diagrams for the
mono disperse frictionless system and poly disperse system with
friction we conclude that the landscape of the poly disperse
system is rougher .
To understand the region labelled as strong, observe that the
image of the interaction network for poly disperse system does
not contain any red simplices, implying that there are no
extremely strong force interactions. In contrast, such red
simplices are present in the mono disperse system. This
difference can be inferred from the 0-dimension persistence
diagrams. The value 1 represents the average interaction force.
For the poly disperse system there are no persistence points
with the birth value larger than 3 and only a few points with
birth value larger than 2.5. Thus, depending on the exact
cut-off there are no or at most few points in the region marked
strong for the poly disperse system system, in clear contrast to
the mono disperse system.
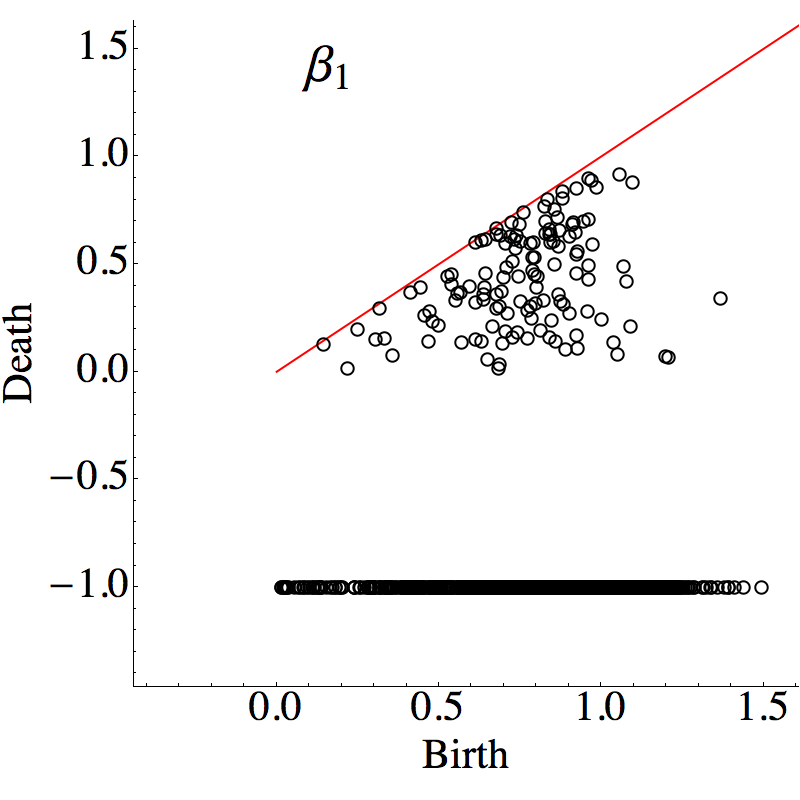
If we take the left division marker for the medium regime to be
1, then the persistence points in the moderate and strong
regions provide information about the geometry of what the DGM
community typically refer to as a force chain. In the case
of the poly disperse system, we see a large number of
points in the 0-dimension persistence diagram that are
born between 1 and 2.5 and die before 0.8. This suggests a
landscape consisting of moderately high peaks separated by
moderately high valleys. To continue the geographic
metaphor, the interaction network of poly disperse system
takes place on a high plateau. In contrast, the mono
disperse system has fewer moderately high peaks, but they are
separated by much deeper valleys since there are points with
death values below $0.6$. Therefore, we conjecture
that the landscape for the mono disperse system has
fewer peaks (but some of them are strong) than that of the poly
disperse system, and these peaks are in general much
more isolated and more likely to be separated by valleys of much
weaker forces.
Finally, we consider the region labelled defects. In a
0-dimension persistence diagram each point in this region
corresponds to a distinct connected component. In the
context of the poly disperse system these mostly
correspond to rattlers. This conclusion is obtained by
observing that aside from the single persistence point with a
large birth force, that corresponds to the component containing
most of the particles, the persistence points in the defects
region have a birth value of 0, indicating that they are not
experiencing any normal force. This is quite different
from the mono disperse system. In this case we have persistence
points in the defects region with non-zero birth forces. This
implies the existence of small clusters of particles (a single
separated particle cannot have an interaction force) that are
not interacting with the dominant particle cluster. Close
inspection of the interaction force network for the mono
disperse system reveals these small components.
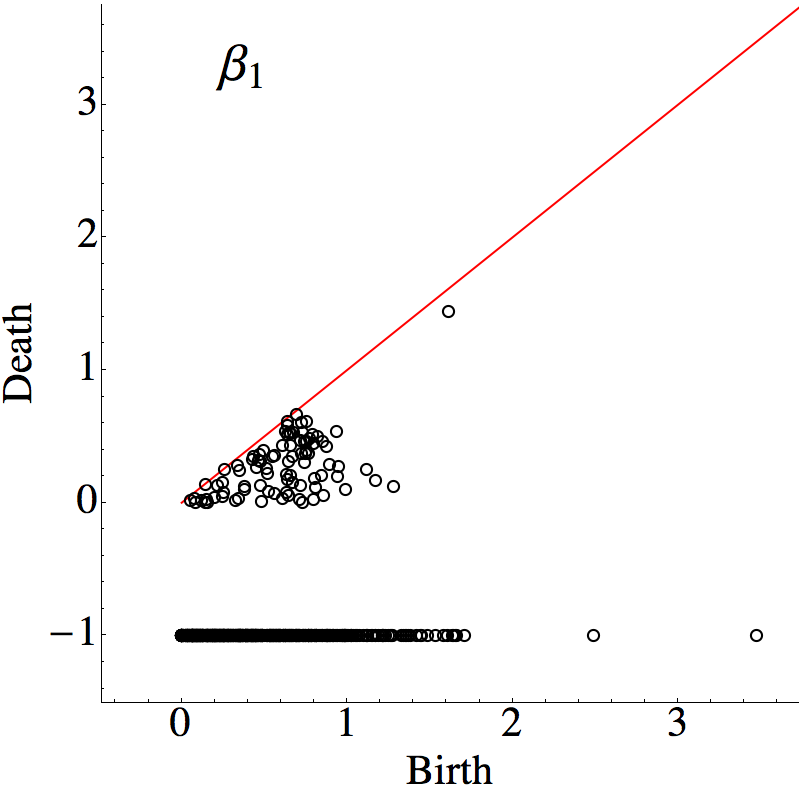
The defects region of the 1-dimension persistence diagrams
provides additional information as explained in our paper.