Overview
Particulate systems
consisting of a large number of particles have attracted
significant attention in the last decades. Despite significant
research on these systems, their properties are still not
well understood and some of them appear to be rather
elusive. The fact that the forces do not propagate uniformly
in the systems made of interacting particles has been established
in a number of different systems, ranging from those where
particles' are on atomic or molecular scales, to those with
macroscopic particles. Very recently, initial attempts have been
made to consider the inter particle forces based on network-type
of analysis, and of by exploring their topological properties.
With the goal of extending our ability to systematically explore
network properties in greater detail, we developed rigorous
mathematical models capable of capturing geometric features
of particle interactions. The approach is based
on algebraic topology and in particular persistent homology.
This is a relatively new mathematical technique that
provides a computationally efficient rigorous framework for
multi scale analysis.
Publications
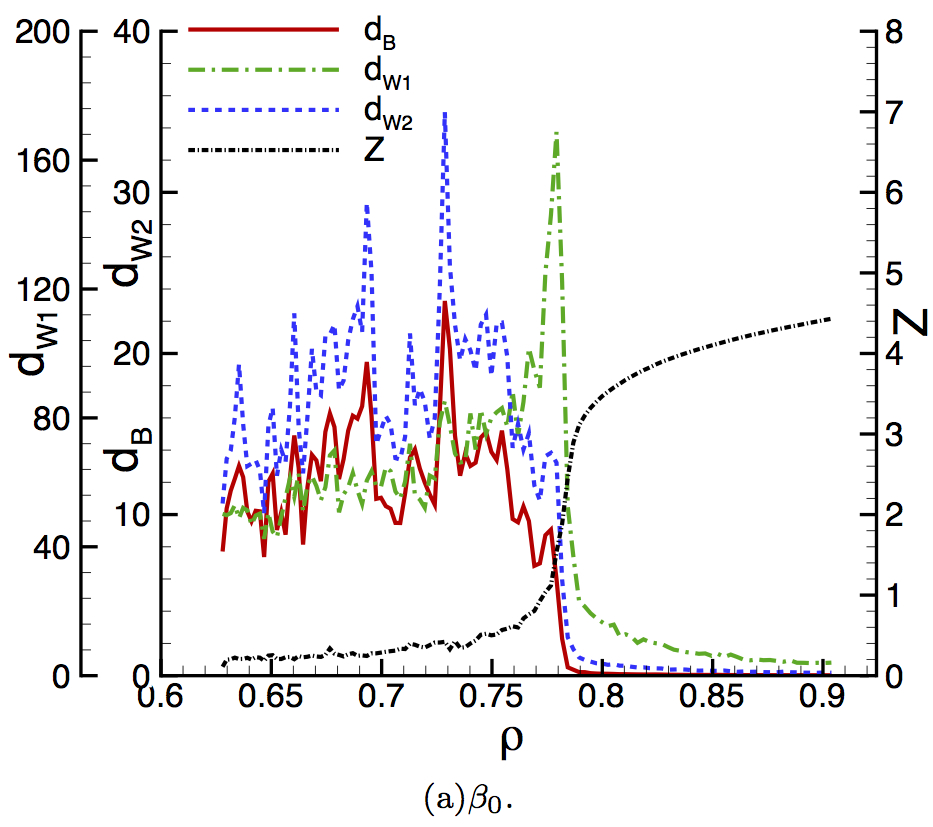
| Evolution of Force Networks in Dense Particulate Media |
|
|---|---|
|
|
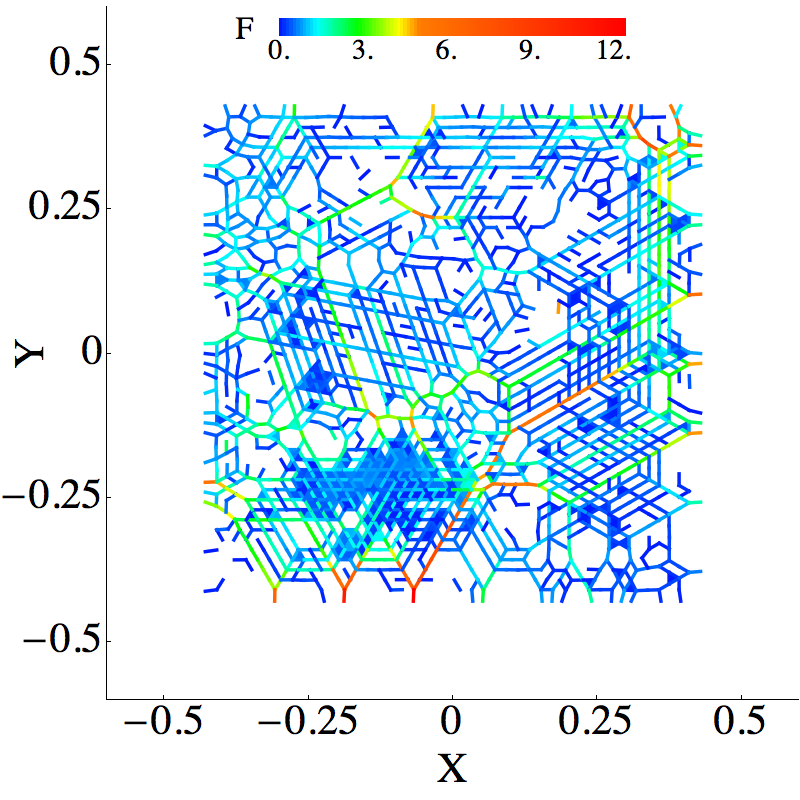
| Quantifying force networks in particulate systems |
|
|
|
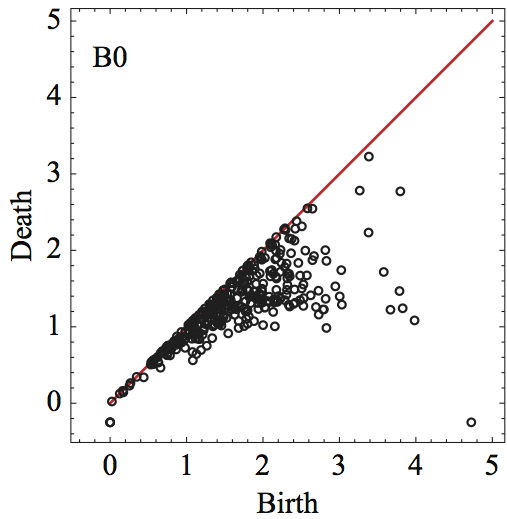
| Persistence of force networks in compressed granular media |
|
|
|
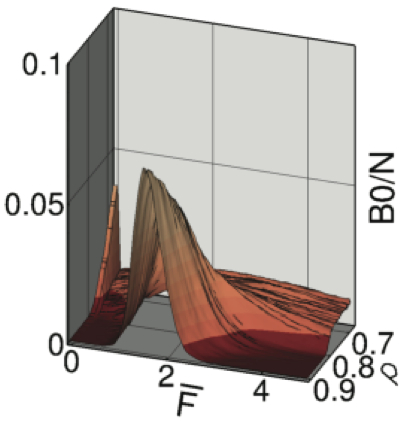
| Topology of force networks in compressed granular media | |
|
|