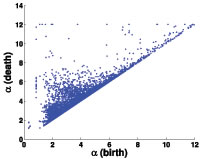
Persistent homology provides an algebraic topological tool for quantifying and characterizing geometric features of objects and functions. Perseus uses ideas from discrete Morse theory to provide an efficient preprocessor for the standard persistent homology algorithm.

In joint work with M. Schatz's group at Georgia Tech and M. Paul's group at Virginia Tech, we are using Raleigh Benard Convection as a model system to advance understanding of complexity when non equilibrium effects come into play. The behaviors of such systems are usually highly non-periodic, lack any symmetries, and appear at a variety of scales; thus, the number of attainable patterns and structures (and the corresponding raw data sets) from these systems is enormous. Our goal is to use algebraic topology to translate data, both experimental and numerical, from complex nonequilibrium systems into knowledge.

Granular materials in the dense fluid-like and solid states present one of the most significant modeling challenges of our times. These materials appear in a broad spectrum of practical settings from heavy industry to pharmaceuticals. As such, they are of intense interest to the engineering world. The way in which grains pack and in which forces are carried in dense granular materials presents a significant puzzle for the soft condensed matter and statistical physics communities. Associated with force and packing complexity are challenging mathematical issues related to the analysis of complex high dimensional multiscale spatiotemporal data. In joint work with L. Kondic's group at NJIT and R. Behringer's group at Duke we are using persistent homology to capture the geometry of these forces.

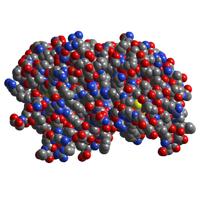
We use persistent Homology to extract geometrical and topological information from protein data available in the Protein Data Bank (PDB). Using the CGAL library we construct Alpha Complexes from the PDB data and then use the Perseus software to compute persistence diagrams.

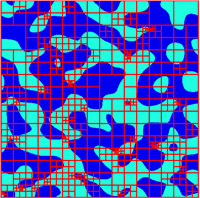
Homology is an important computable tool for quantifying complex structures. In many applications these structures arise as nodal domains of real-valued functions and are therefore amenable only to a numerical study, based on suitable discretizations. Such an approach immediately raises the question of how accurate the resulting homology computations are. In the papers cited below, we present a probabilistic approach to quantifying the validity of homology computations for nodal domains of random Fourier series in one and two space dimensions, which furnishes explicit probabilistic a-priori bounds for the suitability of certain discretization sizes. In addition, we introduce a numerical method for verifying the homology computation using interval arithmetic.

Evolution of Pattern Complexity During Phase Separation

Phase separation processes in compound materials can produce intriguing and complicated patterns. Yet, characterizing the geometry of these patterns quantitatively can be quite challenging. Here we propose the use of computational homology to obtain such a characterization. Our method is illustrated for the complex microstructures observed during spinodal decomposition and early coarsening in both the deterministic Cahn-Hilliard-Cook model. While both models produce microstructures that are qualitatively similar to the ones observed experimentally, our topological characterization points to significant difference. One particular aspect of our method is its ability to quantify boundary effects in finite size systems.

Within this project, quantitative characterizations for the thermal-elastic response of calcite-based polycrystals are developed. The characterization is based on topological measurements such as the number of components and the number of handles of a complex microstructure. These characterizations are then applied to characterize both the grain boundary misorientations in the polycrystal and the resulting elastic energy density and principal stress fields. It is demonstrated that the topological analysis can quantitatively distinguish between different types of grain boundary misorientations, as well as between the resulting differences in the response fields.

It is well established both numerically and experimentally that nonlinear systems involving diffusion, chemotaxis, and/or convection mechanisms can generate complicated time-dependent patterns. Since this phenomenon is global in nature, obtaining a quantitative mathematical characterization that to some extent records or preserves the geometric structures of the complex patterns is difficult. Here we show that using algebraic topology, in particular homology, we can measure Lyapunov exponents that imply the existence of spatial-temporal chaos and suggest a tentative step towards the classification and/or identification of patterns within the FitzHugh-Nagumo system.