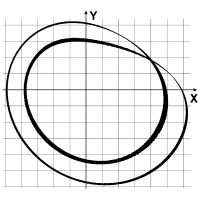
Coarse, topological measurements of dynamical systems defined by maps can be used to uncover information about invariant sets for the system.  These techniques are based on the Conley index and have been used to detect invariant structures from fixed points and periodic orbits, to connecting orbits and sets which exhibit chaotic symbolic dynamics.  More notably, these techniques have been used to study both finite-dimensional and infinite-dimensional systems and to prove the existence of unstable invariant sets. The method relies on first building a pair of compact sets called an index pair and then computing the relative homology of the pair.  This information is then used to make conclusions about the associated invariant structures.  

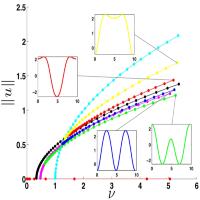
One of the most efficient methods for determining the equilibria of a continuous parameterized family of differential equations is to use predictor-corrector continuation techniques. In the case of partial differential equations this procedure must be applied to some finite dimensional approximation which of course raises the question of the validity of the output. We introduce a new technique that combines the information obtained from the predictor-corrector steps with ideas from rigorous computations and verifies that the numerically produced equilibrium for the finite dimensional system can be used to explicitly define a set which contains a unique equilibrium for the infinite dimensional partial differential equation.

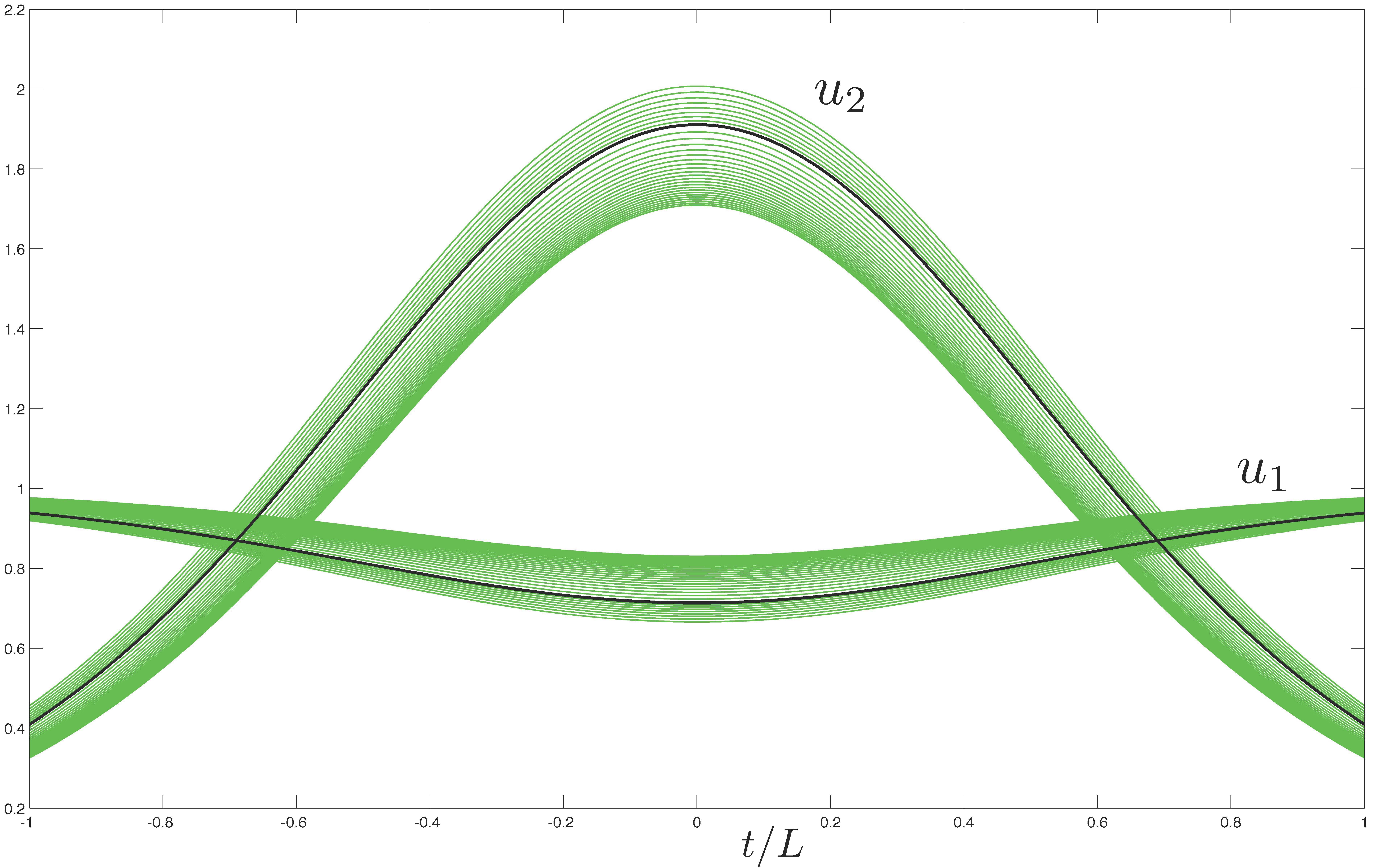
A method based on the Conley index theory for proving the existence of periodic trajectories in a smooth dynamical system in Euclidean space is developed. This method can be applied in the cases where a hyperbolic periodic orbit is numerically observed. The method uses cubical index pairs and requires the computation of the map induced in homology by the cubical index map.

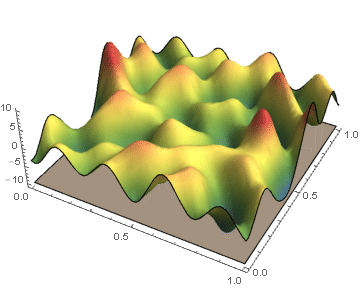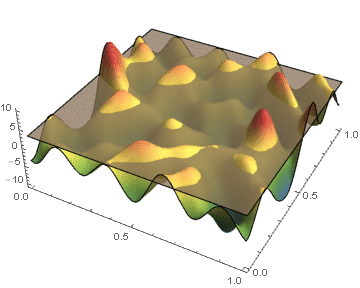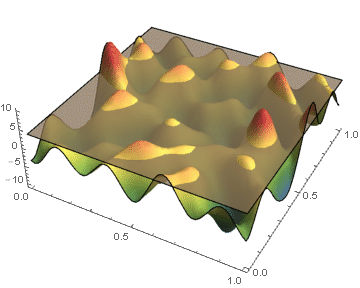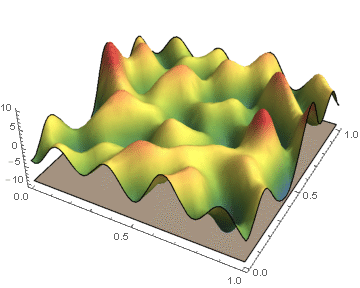
Biological and physical systems often exhibit distinct structures at different spatial/temporal scales. Persistent homology is an algebraic tool that provides a mathematical framework for analyzing the multi-scale structures frequently observed in nature. We develop a theoretical framework for algorithmically computing an arbitrarily good approximation of the persistence generated by the sub-level sets of a real valued functions on CW-complex. We also investigate a priori and a posteriori bounds of the approximation error introduced by our method. In the case where the function's domain is a square, we have developed code which will compute the persistence diagrams of the function, and the associated error bounds.