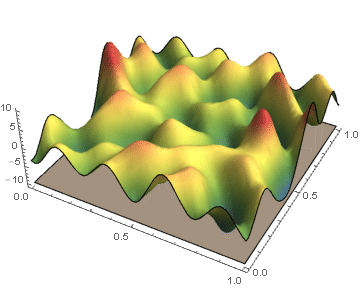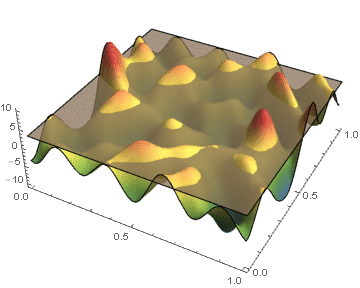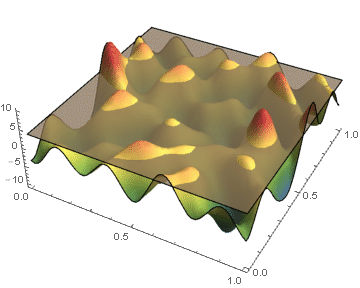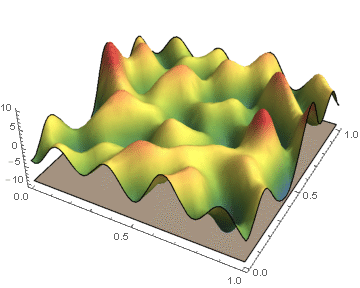
Biological and physical systems often exhibit distinct structures at different spatial/temporal scales. Persistent homology is an algebraic tool that provides a mathematical framework for analyzing the multi-scale structures frequently observed in nature. We develop a theoretical framework for algorithmically computing an arbitrarily good approximation of the persistence generated by the sub-level sets of a real valued functions on CW-complex. We also investigate a priori and a posteriori bounds of the approximation error introduced by our method. In the case where the function's domain is a square, we have developed code which will compute the persistence diagrams of the function, and the associated error bounds.

"On ε-Approximations of Persistence Diagrams " J. Jaquette and M. Kramar, Submitted (2014)

The code associated with this paper can be downloaded here.