Data referred to in the paper
This page contains the information referred to in the paper Graph approach to the computation of the homology of continuous maps by K. Mischaikow, M. Mrozek, and P. Pilarczyk.
In particular, some of the examples contained in the examples subdirectory of the source code of the homology software which are referred to in the paper are described below in details.
Acyclic cubical sets that cannot be reduced
The example called nonred contains two geometric figures which are unions of cubes of maximal dimension, but are difficult to reduce, although they are acyclic, that is, their homology is the homology of a one-point space.
The first example cannot be reduced by means of removing cubes, because the removal of any cube causes the change of the homology of the set. However, this set can be reduced to a single point by means of free face collapses.
The second example is even more complicated. It has the property that the removal of any cube causes the change to its homology, and, moreover, by means of free face collapses it can be reduced to another set of dimension two, but not to a single point.
Note that the example sets mentioned here contain several hundreds of cubes and arose naturally in some experiments with the reduction procedures. Much smaller and more obvious examples are well-known Dunce Hat and Bing's House. Two simple representations of the latter (built of elementary cubes) are included in the CHomP examples of cubical sets.
An acyclic map whose restriction is no longer acyclic
An example called nonacycl shows an acyclic cubical multivalued map F: X -> Y such that its restriction to a subset A of X is not acyclic. Therefore, the map induced by F: (X, A) -> (Y, B) cannot be computed by homcubes.
The sets of interest and the map assignments are defined as follows
(as illustrated in the picture on the right):
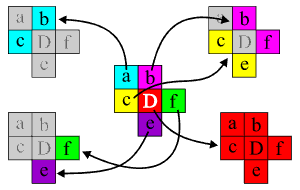
- a = [0,1] x [1,2]
- b = [1,2] x [1,2]
- c = [0,1] x [0,1]
- D = [1,2] x [0,1]
- e = [1,2] x [-1,0]
- f = [2,3] x [0,1]
- X = Y = {a, b, c, D, e, f}
- A = B = {a, b, c, e, f}
- a -> {c, b}
- b -> {b, f}
- c -> {e, c}
- D -> {a, b, c, D, e, f}
- e -> {e}
- f -> {f}
As one can analyze, the image of each elementary cube in the domain is an acyclic set. However, if one removes the cube 'D' from the map's domain, then the common vertex of the cubes 'a', 'b' and 'c' has the image consisting of 'b', 'c', 'e' and 'f', which is not acyclic.
Note that this map has an acyclic selector, for example, the "orthogonal projection" onto the stripe "cDf" (that is, [0,3] x [0,1] if the origin is located at the lower left corner of 'c'). Therefore, the map induced in homology after the removal of 'D' should be the identity.
An acyclic map that loses its acyclicity
An example of a map which seems to be good for homology computation, but the program homcubes reduces the cubes in such a way that after the reduction the map is no longer acyclic is contained in the examples folder under the name probl. If one turns on the careful reduction method which does preserve the acyclicity of the map (this is done by the -a switch), then the program works fine (though slower) and gives the right result. This example was found by Sarah Day in her numerical experiments with the Hénon map.
Note: The above holds true for homcubes version 3.04 as of May 9, 2003, but may not apply to the new revisions of homcubes due to the possible changes in the reduction algorithms.
HomCubes versus ChMap
One of the main motivations in the development of the program homcubes was to replace the program chmap which was very slow and memory-consuming, mainly because it didn't use any geometric reduction. You are welcome to consult a detailed note on the comparison of the two programs.
Benchmarks
For the details on the benchmarks mentioned in the paper, as well as some additional speed and memory usage comparison, you are referred to the Benchmarks page.